朴素贝叶斯复习

　　贝叶斯定理：P(A|B) = P(AB) / P(B)

机器学习重要概念复习：

　　方法 = 模型 + 策略 + 算法
　　损失函数：度量预测错误的程度，有0-1损失函数，平方损失函数，对数损失函数，对数损失函数等。当然越小越好
　　风险函数：就是损失函数的期望，也就是对所有情况下的损失函数的值乘以发生该情况的概率做积分。这个发生该情况的概率是不知道的，知道的话也没有训练的必要了。所以有了平均损失，称为经验风险，也就是训练样本的平均损失。
　　经验风险最小化和结构风险最小化：经验风险最小化是认为经验风险最小那么就是最好的，模型时条件概率分布，损失函数是对数损失函数时，经验风险最小化就等价于极大似然估计（朴素贝叶斯和这个不同，朴素贝叶斯考虑了，不同。如果样本容量小，经验风险最小化会产生过拟合的现象。结构风险最小化，就是为了对付过拟合，结构风险最小化就是正则化，就是在经验风险上加上模型复杂度的正则化项。当模型是条件概率分布，损失函数是对数函数损失，模型复杂度有模型的先验概率表示时，结构风险最小化就等价于最大后验概率估计。

距离度量学习：

　　1.欧式距离:
　　
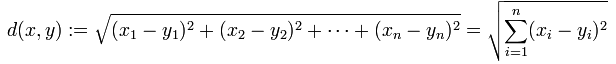
　　2.曼哈顿距离：也就是各个维度差的绝对值的和的距离。
　　3.切比雪夫距离：各个维度的差的绝对值的最大值。是超凸函数的一种，等价形式如下：
　　
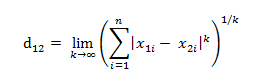
　　4.闵可夫斯基距离，是对上面几种距离的一中归纳。
　　
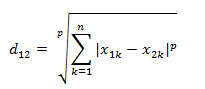
　　其中p是一个变参数。
　　当p=1时，就是曼哈顿距离
　　当p=2时，就是欧氏距离
　　当p趋于无穷时，就是切比雪夫距离
　　根据变参数的不同，闵氏距离可以表示一类的距离。
　　5.标准化欧式距离，标准化欧氏距离是针对简单欧氏距离的缺点而作的一种改进方案。标准欧氏距离的思路：既然数据各维分量的分布不一样，那先将各个分量都“标准化”到均值、方差相等。至于均值和方差标准化到多少，先复习点统计学知识。
　　假设样本集X的数学期望或均值(mean)为m，标准差(standard deviation，方差开根)为s，那么X的“标准化变量”X*表示为：(X-m）/s，而且标准化变量的数学期望为0，方差为1。
　　公式如下：
　　
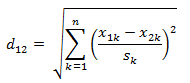
　　如果将方差的倒数看成是一个权重，这个公式可以看成是一种加权欧氏距离(Weighted Euclidean distance)。
　　6.马氏距离
　　有M个样本向量X1~Xm，协方差矩阵记为S，均值记为向量μ，则其中样本向量X到u的马氏距离表示为：
　　
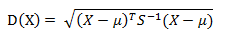
　　而其中向量Xi与Xj之间的马氏距离定义为：
　　
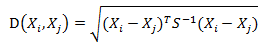
　　若协方差矩阵是单位矩阵（各个样本向量之间独立同分布），那么马氏距离和欧式距离就一样了。马氏距离可以排除变量之间的相关性的干扰。
　　7.巴氏距离
　　8.汉明距离